Functional Reactive Programming (FRP) is a paradigm that has simplified the construction of reactive programs. There are many libraries that implement incarnations of FRP, us- ing abstractions such as Applicative, Monads, and Arrows. However, finding a good control flow, that correctly manages state and switches behaviors at the right times, still poses a major challenge to developers.
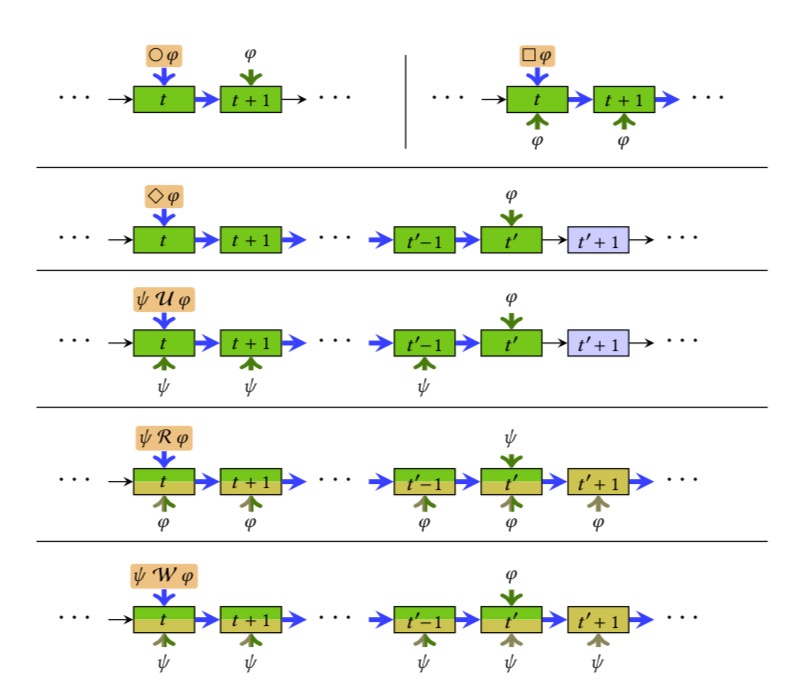
An attractive alternative is specifying the behavior instead of programming it, as made possible by the recently devel- oped logic: Temporal Stream Logic (TSL). However, it has not been explored so far how Control Flow Models (CFMs), resulting from TSL synthesis, are turned into executable code that is compatible with libraries building on FRP. We bridge this gap, by showing that CFMs are a suitable formalism to be turned into Applicative, Monadic, and Arrowized FRP.
We demonstrate the effectiveness of our translations on a real-world kitchen timer application, which we translate to a desktop application using the Arrowized FRP library Yampa, a web application using the Monadic Threepenny-GUI library, and to hardware using the Applicative hardware description language ClaSH.
This work, Synthesizing Functional Reactive Programs, has been accepted to Haskell 2019. This is a joint work with Bernd Finkbeiner, Felix Klein, Ruzica Piskac, and Mark Santolucito.
Constraint solvers give programmers a useful interface to solve challenging constraints at runtime. In particular, SMT solvers have been used for a vast variety of different, use- ful applications, ranging from strengthening Haskell’s type system to verifying network protocols.
Unfortunately, interacting with constraint solvers directly from Haskellrequires a great deal of manual effort. Data must be represented in and translated between two forms: that un- derstood by Haskell, and that understood by the SMT solver. Such a translation is often done via printing and parsing text, meaning that any notion of type safety is lost. Furthermore, direct translations are rarely sufficient, as it typically takes many iterations on a design in order to get optimal – or even acceptable – performance from a SMT solver on large scale problems. This need for iteration complicates the translation issue: it is easy to introduce a runtime bug and frustrating to fix said bug.
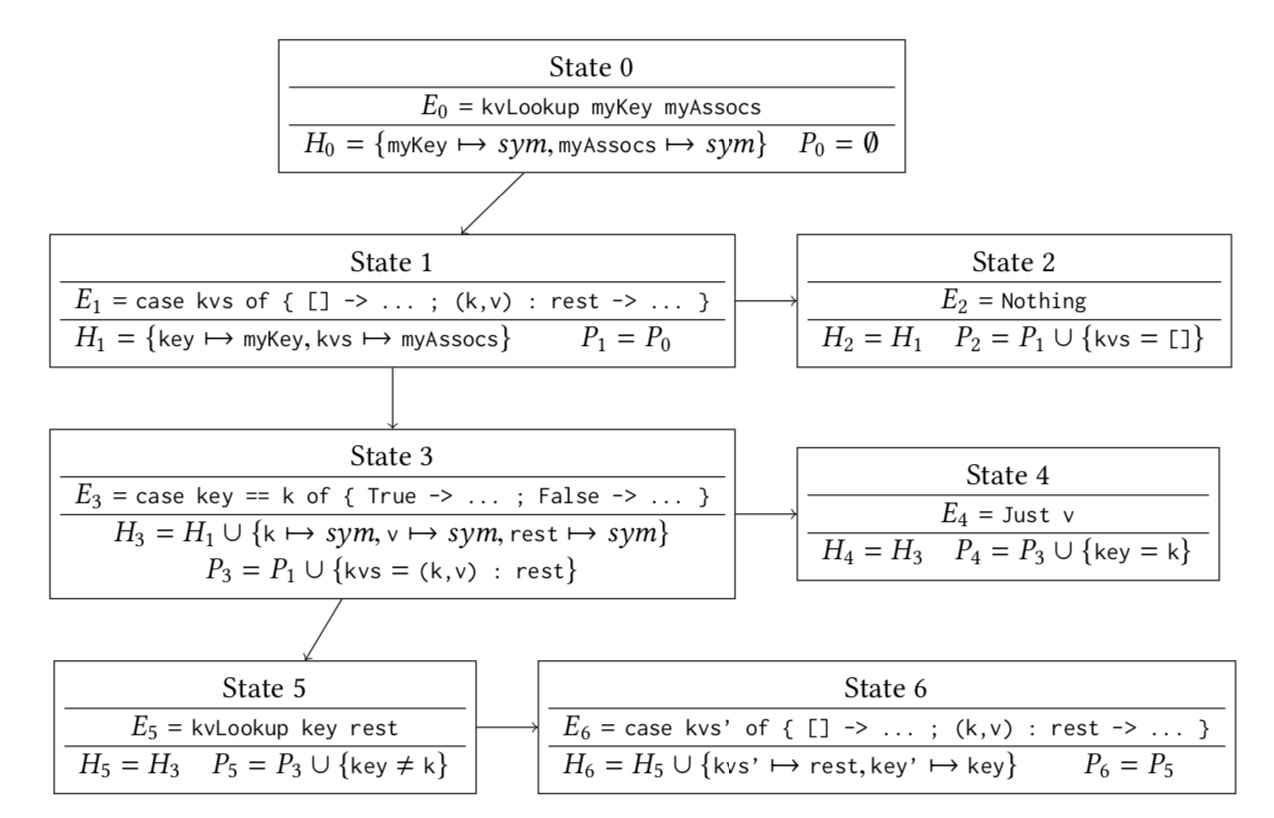
To address these problems, we introduce a new constraint solving library, G2Q. G2Q includes a quasiquoter that allows solving constraints written in Haskell itself, thus unifying data representation, ensuring correct typing, and simplifying development iteration. We describe the API to our library and its backend. Rather than a direct translation to SMT formulas,G2Q makes use of the G2 symbolic execution engine. This allows G2Q to solve problems that are out of scope when directly encoded as SMT formulas. Finally, we demonstrate the usability of G2Q via four example programs.
This work, G2Q: Haskell Constraint Solving, has been accepted to Haskell 2019. This is a joint work with William T. Hallahan, Anton Xue, and Ruzica Piskac.